昨日は「将棋界で1年で一番長い日」、A級順位戦の最終局がおこなわれました。結果は・・
ちょっと解説します。
将棋界の頂点は「名人」です。現在の名人は佐藤天彦さんです。
名人になるには挑戦者となって七番勝負で4勝することが必要です。
挑戦者になるにはA級順位戦(原則10名が参加)という総当たりのリーグ戦で1位になることが条件です。
A級順位戦に出場するにはB級1組というリーグ戦で2位以内になることが条件です。
以下、B級2組・C級1組・C級2組・C級3組とクラスが分かれていて、上位2人(C級2組は3人)が毎年昇級するというルールです。つまり、A級になるには最短でも5年かかります。
また、A級とB級1組は下位2人が翌年は降級します。B級2組以下は下位20%になると降級点がついて、降級点2個で降級(C級3組は3個でフリークラスへ転出)します。
こういうルールがあるので、将棋のトーナメントプロの人数はほぼ一定に保たれています。
さて、今年のA級順位戦は昨年の三浦九段への八百長冤罪事件の影響で11名でおこなわれました。昨日、その最終局の一斉対局がおこなわれたのですが、この結果が、なんと6人が6勝4敗で並ぶという前代未聞の珍事となりました。6人でプレーオフとなります。
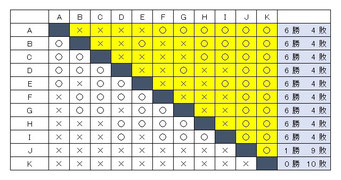
さて、11人の総当たりリーグ戦では最大で何人が首位に並ぶことができるでしょうか?
答えは、9人です。例えば、右の表のような勝敗表になります。
それでは、例年の10人参加の総当たりでは何人が首位に並ぶことができるでしょうか?
答えは8人です。実際の歴史では4人が同じ勝数で並んだことが最大だそうです。
11人の総当たり戦の試合数は11×10÷2=55ですから、勝数の合計も55です。1位になれる最少の勝数は6ですから、55÷6=9.17>9 となり、9人が最大(54勝)です。
10人の総当たり戦は同様に45勝を分け合って、最少の勝数は5勝ですから45÷5=9になるので9人が5勝(残る1人が全敗)で並べそうに思えます。しかし、この場合は全敗の1人を除く9人の相互の試合数が9×8÷2=36となって9で割り切れないので成立しません。
それにしても、1年間戦って、最後に多数でプレーオフというのも辛いです。サッカーなどでは勝ち点制とか得失点差で決まるのですが、将棋では難しいですね。
